Introduction

Poker hand ranking combinations Clip Art - Fotosearch Enhanced. K30655968 Fotosearch Stock Photography and Stock Footage helps you find the perfect photo or footage, fast! We feature 64,300,000 royalty free photos, 342,000 stock footage clips, digital videos, vector clip art images, clipart pictures, background graphics, medical illustrations. In poker, players form sets of five playing cards, called hands, according to the rules of the game. Each hand has a rank, which is compared against the ranks of other hands participating in the showdown to decide who wins the pot. In high games, like Texas hold 'em and seven-card stud, the highest-ranking hands win. Combinatorics of Sets. One reason sets are so valuable is because of how unlikely they are to occur. The 3 and 2 are on the flop, which means that Rafi’s range has made a set with two of his pre-flop hands (33 and 22). With one of each card on the flop, the number of combinations for 33 and 22 are cut in half (from 6 combinations to 3). For a great training video on poker combinatorics, check out this poker combos video. 'Combinatorics' is a big word for something that isn’t all that difficult to understand. In this article, I will go through the basics of working out hand combinations or 'combos' in poker and give a few examples to help show you why it is useful.

Derivations for Five Card Stud

I have been asked so many times how I derived the probabilities of drawing each poker hand that I have created this section to explain the calculation. This assumes some level mathematical proficiency; anyone comfortable with high school math should be able to work through this explanation. The skills used here can be applied to a wide range of probability problems.

The Factorial Function

If you already know about the factorial function you can skip ahead. If you think 5! means to yell the number five then keep reading.

The instructions for your living room couch will probably recommend that you rearrange the cushions on a regular basis. Let's assume your couch has four cushions. How many combinations can you arrange them in? The answer is 4!, or 24. There are obviously 4 positions to put the first cushion, then there will be 3 positions left to put the second, 2 positions for the third, and only 1 for the last one, or 4*3*2*1 = 24. If you had n cushions there would be n*(n-1)*(n-2)* ... * 1 = n! ways to arrange them. Any scientific calculator should have a factorial button, usually denoted as x!, and the fact(x) function in Excel will give the factorial of x. The total number of ways to arrange 52 cards would be 52! = 8.065818 * 10⁶⁷.

The Combinatorial Function

Poker Combinations Printable Chart

Assume you want to form a committee of 4 people out of a pool of 10 people in your office. How many different combinations of people are there to choose from? The answer is 10!/(4!*(10-4)!) = 210. The general case is if you have to form a committee of y people out of a pool of x then there are x!/(y!*(x-y)!) combinations to choose from. Why? For the example given there would be 10! = 3,628,800 ways to put the 10 people in your office in order. You could consider the first four as the committee and the other six as the lucky ones. However you don't have to establish an order of the people in the committee or those who aren't in the committee. There are 4! = 24 ways to arrange the people in the committee and 6! = 720 ways to arrange the others. By dividing 10! by the product of 4! and 6! you will divide out the order of people in an out of the committee and be left with only the number of combinations, specifically (1*2*3*4*5*6*7*8*9*10)/((1*2*3*4)*(1*2*3*4*5*6)) = 210. The combin(x,y) function in Excel will tell you the number of ways you can arrange a group of y out of x.

Now we can determine the number of possible five card hands out of a 52 card deck. The answer is combin(52,5), or 52!/(5!*47!) = 2,598,960. If you're doing this by hand because your calculator doesn't have a factorial button and you don't have a copy of Excel, then realize that all the factors of 47! cancel out those in 52! leaving (52*51*50*49*48)/(1*2*3*4*5). The probability of forming any given hand is the number of ways it can be arranged divided by the total number of combinations of 2,598.960. Below are the number of combinations for each hand. Just divide by 2,598,960 to get the probability.

Poker Math

The next section shows how to derive the number of combinations of each poker hand in five card stud.

Royal Flush

There are four different ways to draw a royal flush (one for each suit).

Poker Combinations Printable Sheets

Straight Flush

The highest card in a straight flush can be 5,6,7,8,9,10,Jack,Queen, or King. Thus there are 9 possible high cards, and 4 possible suits, creating 9 * 4 = 36 different possible straight flushes.

Four of a Kind

There are 13 different possible ranks of the 4 of a kind. The fifth card could be anything of the remaining 48. Thus there are 13 * 48 = 624 different four of a kinds.

Full House

There are 13 different possible ranks for the three of a kind, and 12 left for the two of a kind. There are 4 ways to arrange three cards of one rank (4 different cards to leave out), and combin(4,2) = 6 ways to arrange two cards of one rank. Thus there are 13 * 12 * 4 * 6 = 3,744 ways to create a full house.

Flush

There are 4 suits to choose from and combin(13,5) = 1,287 ways to arrange five cards in the same suit. From 1,287 subtract 10 for the ten high cards that can lead a straight, resulting in a straight flush, leaving 1,277. Then multiply for 4 for the four suits, resulting in 5,108 ways to form a flush.

Straight

The highest card in a straight can be 5,6,7,8,9,10,Jack,Queen,King, or Ace. Thus there are 10 possible high cards. Each card may be of four different suits. The number of ways to arrange five cards of four different suits is 4⁵ = 1024. Next subtract 4 from 1024 for the four ways to form a flush, resulting in a straight flush, leaving 1020. The total number of ways to form a straight is 10*1020=10,200.

Three of a Kind

There are 13 ranks to choose from for the three of a kind and 4 ways to arrange 3 cards among the four to choose from. There are combin(12,2) = 66 ways to arrange the other two ranks to choose from for the other two cards. In each of the two ranks there are four cards to choose from. Thus the number of ways to arrange a three of a kind is 13 * 4 * 66 * 4² = 54,912.

Two Pair

There are (13:2) = 78 ways to arrange the two ranks represented. In both ranks there are (4:2) = 6 ways to arrange two cards. There are 44 cards left for the fifth card. Thus there are 78 * 6² * 44 = 123,552 ways to arrange a two pair.

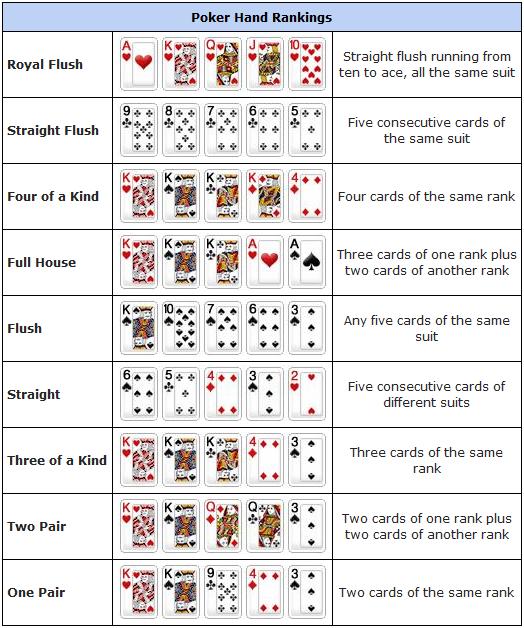
One Pair

There are 13 ranks to choose from for the pair and combin(4,2) = 6 ways to arrange the two cards in the pair. There are combin(12,3) = 220 ways to arrange the other three ranks of the singletons, and four cards to choose from in each rank. Thus there are 13 * 6 * 220 * 4³ = 1,098,240 ways to arrange a pair.

Nothing

First find the number of ways to choose five different ranks out of 13, which is combin(13,5) = 1287. Then subtract 10 for the 10 different high cards that can lead a straight, leaving you with 1277. Each card can be of 1 of 4 suits so there are 4⁵=1024 different ways to arrange the suits in each of the 1277 combinations. However we must subtract 4 from the 1024 for the four ways to form a flush, leaving 1020. So the final number of ways to arrange a high card hand is 1277*1020=1,302,540.

Specific High Card

For example, let's find the probability of drawing a jack-high. There must be four different cards in the hand all less than a jack, of which there are 9 to choose from. The number of ways to arrange 4 ranks out of 9 is combin(9,4) = 126. We must then subtract 1 for the 10-9-8-7 combination which would form a straight, leaving 125. From above we know there are 1020 ways to arrange the suits. Multiplying 125 by 1020 yields 127,500 which the number of ways to form a jack-high hand. For ace-high remember to subtract 2 rather than 1 from the total number of ways to arrange the ranks since A-K-Q-J-10 and 5-4-3-2-A are both valid straights. Here is a good site that also explains how to calculate poker probabilities.

Five Card Draw — High Card Hands

Hand	Combinations	Probability
Ace high	502,860	0.19341583
King high	335,580	0.12912088
Queen high	213,180	0.08202512
Jack high	127,500	0.04905808
10 high	70,380	0.02708006
9 high	34,680	0.01334380
8 high	14,280	0.00549451
7 high	4,080	0.00156986
Total	1,302,540	0.501177394

Ace/King High

For the benefit of those interested in Caribbean Stud Poker I will calculate the probability of drawing ace high with a second highest card of a king. The other three cards must all be different and range in rank from queen to two. The number of ways to arrange 3 out of 11 ranks is (11:3) = 165. Subtract one for Q-J-10, which would form a straight, and you are left with 164 combinations. As above there 1020 ways to arrange the suits and avoid a flush. The final number of ways to arrange ace/king is 164*1020=167,280.

Internal Links

For lots of other probabilities in poker, please see my section on Probabilities in Poker.

Written by:Michael Shackleford

Summary

Students learn how to use permutations and combinations and when it is appropriate to use each.

Background for Teachers

I will just need a pack of cards, a handful of dice (with various numbers of sides) and a whiteboard. Any examples I use will be listed below.

Student Prior Knowledge

Students should have some familiarity with the factorial.

Intended Learning Outcomes

Students will understand the fundamental differences between permutations and combinations and be able to use this knowledge to determine when a permutation is to be used and when a combination is to be used.

Instructional Procedures

I will begin with the dice, looking to teach the fundamental counting principle. I will use a d6, d8, and d20, rolling the smallest die first and ask my students how many combinations of numbers I can get rolling these dice. In rolling the first dice, how many possible numbers can I get? Rolling the second, and then the third? Give students time to work out a solution. Once they have an idea worked up, state the fundamental counting principle: If 2 events occur in order and the first can occur in m ways, while the second can occur in n ways (after the first has occurred) the two events can occur in order in m*n ways. Proceed through more examples, asking specific students. When they respond, I will ask them how they calculated that answer. Let's say I'm working with a drum machine that contains 11 different bass drum samples. On the bass drum channel, I can apply 1 of 4 different effects (distortion, reverb, delay, chorus), how many different bass drum sounds can I get out of this drum machine? Now that I'm done working on my drum machine, I hear the ice cream man coming. He's got 3 different cones and 5 different flavors, how many different ice cream treats can I get? After all of that ice cream, I'm parched. I head to the Kwik-e-mart where they have 21 different kinds of soda on tap with 6 different add-in flavors (cherry, vanilla, etc.), how many different kinds of drink can I get? Do we count no add-in as an option? Once the students seem comfortable with the fundamental counting principle, we can begin discussing permutations. I tell the students that I have just 10 songs on my iPod (a blatant lie, but I don't want them to deal with numbers that are too big). If I put my iPod on shuffle so it will randomly pick a which song plays, and it won't play a song again until it has gone through all of them, I ask my students how many possible sequences of songs are there if I listen until all 10 are played? I don't think 'a lot' is an acceptable answer. If they don't seem to be moving towards an answer, I'll remind them of the principle we just learned. How many possible first songs are there? (psst, 10) Having played the first song, how many possible second songs are there? And so on. There is a connection here between this concept of permutation and the counting principle we've learned. The first song is the first event that can occur, the second song is the second event and on it goes, so we just keep multiplying 10*9*8*...*3*2*1. I will ask if this loooks familiar to anyone? Does it, possibly, make you want to EXCLAIM, 'I know what that is!!!' It's a factorial. Factorials are what we use to calculate permutations. If I have n objects, I can have n! permutations of those objects. That's the key part to remember. If I have 10 songs, I can have 10! (3,628,800) possible sequences of songs while listening on shuffle--seems like a lot for just 10 songs. Now, let's say I want to make a playlist of 3 of those 10 songs. It could be any 3 distinct songs, but the order of the playlist does matter--that is if I have 2 playlists with the same 3 songs, but they are in a different order in each playlist, then those are different playlists. If I just had 3 songs to choose from altogether, how many different playlists of 3 could I make? How many different songs could be the first song, and once that is set how many could be the second, etc. I could end up with 3! (or 6) different playlists. But I've got more than 3 songs to choose from, so if I've got 10 songs on my ipod, how many different songs could be the first and how many could be the second? How many distinct 3-song playlists could I come up with from my massive library of 10 songs? I would have 10*9*8 = 720. So how might we calculate this? How could we come up with a formula that will give me a permutation of r objects selected from n objects. The following section consists of a number of questions designed to guide students to the formula for 'n choose r permutations.' Sufficient wait time should be used after each question to see if the students can come up with the formula on their own. In the case of my playlist, I wanted to make a 3-song playlist (r = 3) from 10 songs (n = 10), and we ended up multiplying the last 3 terms of the factorial together. How could we express that in a general notation, in terms of n and r? How about reduction of fractions. If I wanted to calculate this 'choose 3 from 10' permutation, I might write it as (1*2*3*4*5*6*7*8*9*10)/(1*2*3*4*5*6*7), or more concisely, 10!/7!. Can we relate these back to n and r? The general formula is n!/(n - r)! because by dividing by (n -- r)! we are reducing it to just the last r terms of n! This is how we calculate 'from n objects, choose r.' It is usually written as P(n, r). Now what about dealing cards? I ask, if I deal a poker hand (5 cards) from a deck of 52 cards, how many permutations would I have? Wait for response, students should answer 52!/47! = 311,875,200. That's how many permutations of cards could be dealt. Remind the students, though, that it doesn't matter what order the cards are dealt in. A full house is still a full house, no matter how the cards were dealt. I ask students how many permutations (just in factorial notation) would there be of the 5 cards that are dealt--just looking at those 5 cards alone? It would be 5! permutations, but each of those 5! permutations is just a different arrangement of a single combination. A combination is like permutation, but order doesn't matter. A hand consisting of the ace of spades, queen of hearts, 2 of clubs, jack of diamonds, and 7 of hearts is exactly the same as a hand consisting of the queen of hearts, jack of diamonds, ace of spades, 7 of hearts, and 2 of clubs--and neither will get you anywhere in poker. There are significantly fewer combinations than there are permutations. In fact, in this example, for every 1 combination, there are 5! permutations. Thus, if we were to find a general formula for picking combinations of r objects from a set of n objects, we would come up with P(n, r)/r!, or more formally, C(n, r) = n!/(r!*(n -- r)!). Notice that C(n, r) is how we write combination of r from n. I will then ask my students, what is the important distinction between permutations and combinations? Their answer should be somewhere along the lines of whether order matters or not. Students will pair up into squish groups and then work the following examples. Each group will raise their hands once they've got an answer and I will call on someone once all groups have their hands up. To answer, students need to identify whether a permutation should be used, or a combination, evaluate the answer, and describe the steps they took to arrive at that answer. In how many different ways can 6 people be seated in a row of 6 chairs? (6! = 720, permutation) In how many ways can 3 pizza toppings be chosen from a selection of 12? (12!/(9!*3!) = 220, combination) If 100 people sign up to be beta testers for a new program, and only 4 are chosen, how many different groups of 4 could there be to beta test the program? (100!/(96!*4!) = 3,921,225, combination) In how many ways can a president, vice president, secretary, and treasurer be chosen from a class of 30? (30!/26! = 657,720, permutation) Once this exercise is done, assign homework and let the students be on their way.

Poker Combinations Printable Worksheets

Strategies for Diverse Learners

By drawing upon a wide variety of examples, I hope to engage all students by appealing to personal interests. When students get to see this kind of mathematics in action, they are more apt to learn it.

Poker Combinations Printable Sheet

Assessment Plan

tudents will assess themselves and their squish partners during the example exercises at the end of the class. I will also be wary of student responses during this time and try to catch any misconceptions or groups that don't have the right answers. A bell quiz the following class day will consist of the question: How many 5-card hands can be dealt from a deck of 52 cards? We will also cover the homework the next day, allowing students to self-evaluate their work.

Poker Combinations Printable